Antes de leer este post aviso, esta solución es barata pero muy mala, con una salida plagada de ruido. Para aplicaciones que necesiten mejor conversión es mejor adquirir un DAC que lo haga. Sin embargo para «cacharrear» es una buena solución.
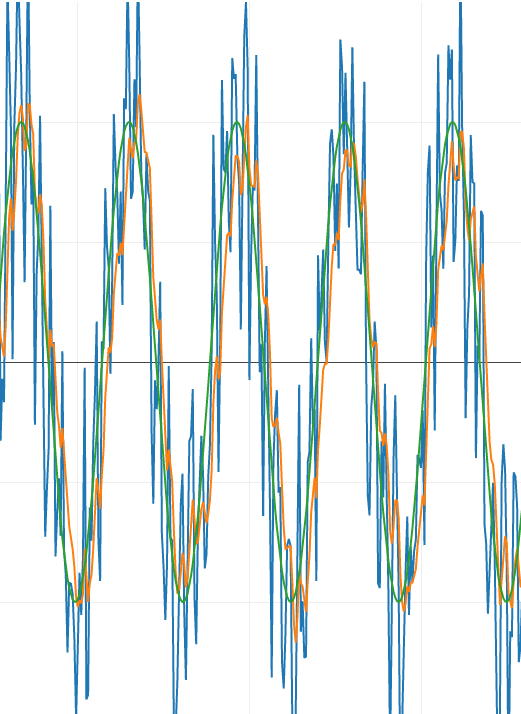
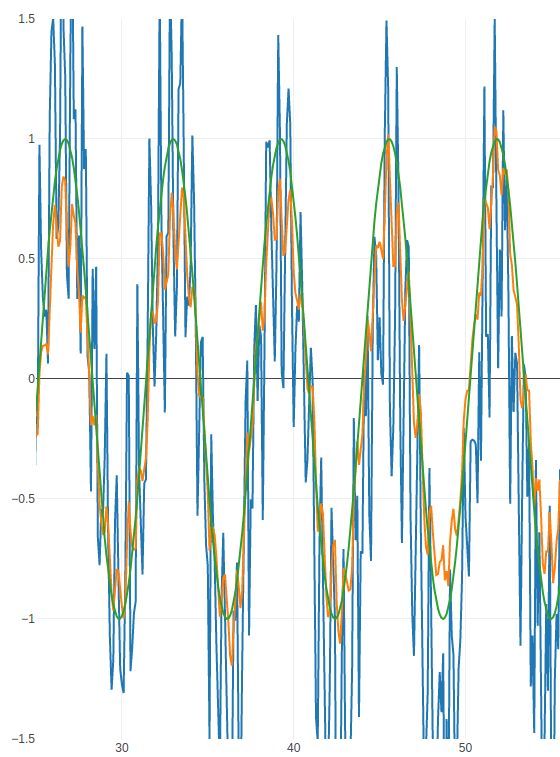
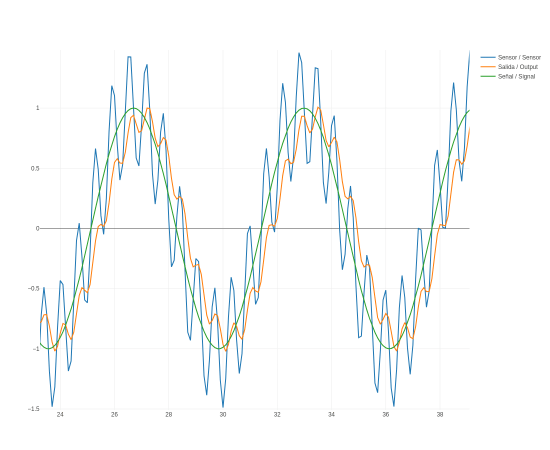
Una de las pegas que encuentro a Arduino UNO es no tener una verdadera salida analógica, que permita devolver un voltaje entre 0v y 5v. Lo más parecido que tenemos es PWM que codifica el valor en forma de la anchura (duración) del pulso. Sin embargo es posible convertir esa señal a voltaje. Vamos a ver cómo conseguir una verdadera salida analógica, variación de voltaje, en Arduino UNO conectando un circuito RC (resistencia condensador) muy sencillo a la salida PWM. La parte teórica del asunto es que el circuito RC actúa como un filtro de paso bajo para filtrar la señal PWM y convertirla en un voltaje constante (más o menos). Usando mi simulador de filtros veamos gráficamente lo que ocurre cuando aplicamos a una señal cuadrada un filtro paso bajo con una frecuencia de corte unas 50 veces menor que la señal cuadrada (En el simulador elegimos como señal una onda cuadrada, filtro paso bajo, una frecuencia para el filtro de 0.0075 Hz y quitamos todas las fuentes de ruido el ruido). El resultado es una señal que tras un periodo tiende a ser estabilizarse alrededor de un valor:

Ese valor será proporcional al tamaño en anchura de la parte alta del pulso cuadrado. Por lo que podemos convertir una pulso PWM, que modula su valor como la anchura de la parte alta de la señal, en un voltaje.
El circuito tiene la siguiente forma: (ahora veremos de donde salen esos valores)

Como ya vimos, para calcular la frecuencia de un filtro paso bajo podemos usar la siguiente formula:
f = 1 / (2* Pi * R * C)
Siendo f la frecuencia, C la capacidad del condensador y R la resistencia.
Para nuestro caso f = 1 / (2 * Pi * 4400 * 10^-7) = 361.71 Hz
Pero hemos dicho que la frecuencia de corte ha de ser unas 50 veces menor que la funcionamiento…pero eso es en la teoría. Haciendo pruebas en la vida real va mejor con alrededor de 100 veces. Por lo que PWM debería funcionar a unos 36 kHz. El problema esta que PWM no trabaja a esa frecuencia….a no ser que la cambiemos como vimos en esta entrada Por lo que fijaremos su frecuencia en unos 32 kHz.
El código será el siguiente:
const byte PRESCALER2 = 0b001;
void setup() {
TCCR2B = (TCCR2B & 0b11111000) | PRESCALER2;
pinMode(3, OUTPUT);
}
void loop() {
analogWrite(3, 255); //5v
delay(5000);
analogWrite(3, 204); //4v
delay(5000);
analogWrite(3, 153); //3v
delay(5000);
analogWrite(3, 102); //2v
delay(5000);
analogWrite(3, 51); //1v
delay(5000);
analogWrite(3, 0); //0v
delay(3000);
}
El resultado tiene bastante ruido y los valores resultantes no son muy exactos. Por lo que no se puede usar para casos donde se requiera gran precisión en el valor.
Para ajustar más los valores podemos usar una pequeña corrección para subir el valor del la señal PWM en los valores más bajos (son los que más se descuadran) y que se aproxime al valor de voltaje que debería tener:
void analog(byte value){
value += (255 - value) >> 4;
analogWrite(3, value);
}
El ejemplo anterior con esta pequeña corrección:
const byte PRESCALER2 = 0b001;
void setup() {
TCCR2B = (TCCR2B & 0b11111000) | PRESCALER2;
pinMode(3, OUTPUT);
}
void loop() {
analog(255); //5v
delay(5000);
analog(204); //4v
delay(5000);
analog(153); //3v
delay(5000);
analog(102); //2v
delay(5000);
analog(51); //1v
delay(5000);
analog(0); //0v
delay(3000);
}
void analog(byte value){
value += (255 - value) >> 4;
analogWrite(3, value);
}
Puedes ver un vídeo sobre este artículo, con demostración del funcionamiento, en mi canal de Youtube: